Number System 2|Theory|Number representation,even odd number
meette
In previous posts we saw some broad classification of numbers. But those classifications are one of many ways numbers can be classified. With each classification more and more concepts come to play which can be tested during an exam. I want my readers to understand that for a chapter like number system there are never enough concepts you can learn and never enough problems you can solve. In such a scenario it is a must that your basics be crystal clear. Apart from my posts here you can also go through the ncert books if you need detailed understanding.
Even Numbers and Odd numbers
Numbers which are divisible by 2 are even numbers and which are not divisible by 2 are odd numbers. One thing we have to keep in mind whenever we use the terms even, odd, prime the numbers are integers mostly whole numbers. From here on our concepts of number system will rarely include fractions.
Rules of even and odd numbers
- Sum of any number of even numbers is always even. Actually instead of a plus we can also have a minus. So even ± even = even
- product of any number of numbers with an even number is always even.
- sum of two odd numbers is even.
- Product of two odd numbers is odd.
- Odd number raised to any power is always odd as it is only a product of a series of odd numbers.
- sum( or difference ) of an even number and odd number is always odd.
- The sum of a odd number of odd numbers is always odd but the sum of even number of odd numbers is even (like in point 3).
- Extending the rules above, in a cluster of numbers containing series of even and odd numbers, whether the net result will be even or odd will depend on the number of odd numbers, not on even numbers. Refer to the examples below.
If there is a cluster like a+b-c-e+m+f-g. What is the net result, even or odd if we know there are 3 odd numbers?
Ans: The result is odd as there are odd number of odd numbers so there net result will be odd and when you add this odd number to the even numbers result will be once again odd.
If you know the proper rules of even and odd the problems will be a cake walk for you.
An even number raised to any whole number power is always even? true or false
Ans: False if the power is 0.
An even number is written as 2n and odd numbers as 2n+1. This is the divisor/remainder representation of a number. For even numbers the remainder is 0 and for odd numbers it is 1. The divisor/remainder representation of a number is a crucial concept which has several applications.
Divisor/Remainder representation of a number
Whenever we divide a number by another number we get a quotient and a remainder. The number itself is called a dividend. So for a number N when divided by D, we get a quotient Q and remainder R.
N=DxQ + R
It literally means when we multiply D with Q we get a number which R less than the number N. R is always 0≤ R< N.
So for example when a number is divided by 3 the only remainders possible are 0,1,2. So any number must be of any one of the forms 3n, 3n +1,3n+2.
No when a number is divide
d by 4 the remainders possible are 0,1,2,3 . So the very same number must also be any one of the forms 4n, 4n +1,4n+2,4n+3.
For 5 it will 5n,5n+1,5n+2,5n+3,5n+4.
We can see that the remainders range from 0 to one less than the divisor. Also we need to remember that 'n' here is merely representational. Obviously the values of n will differ in each divisor/remainder representation.
For eg. the number 46 is of the forms 2n, 3n+1, 4n+2, 5n+1, 6n+4 and so on.
What is the difference between 5n+2 and 5n+7?
Ans: If we take a particular value of n then obviously the numbers are different. But here we are not talking about algebraic expressions rather about number representations and in that case they are same. If we take out a 5 from 7 then 2 is left as a remainder. We have seen that the remainder needs to be expressed as less than the divisors.
So 5n+7=5n+5+2=5(n+1)+2~5k+2.
So 5n+2, 5n+7,5n+12,5n+17 and so on are same representations. (notice the terms increase in arithmetic progression with common difference 5. )
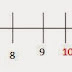
What is the difference between 5n+2 and 5n-3?
Ans.They are the same representation. See the number line below.
The number 7 can be represented as 5x1 +2 and also as 5x2-3. Also the number 9 can be 5x1+4 or 5x2-1. So the negative remainder is nothing but divisor - positive remainder.
When 46 is added to a perfect square number then another perfect square number is obtained. How many cases are there?
Ans: Let
m²+46=n² then n²-m²=46
(n+m)(n-m)=46
n m n+m n-m (n+m)(n-m) valid?
even even even even even may be
odd odd odd odd odd not possible as 46 is even
even odd odd odd odd not possible as 46 is even
odd even odd odd odd not possible as 46 is even
Let n=2a and m=2b then (n+m)(n-m) is 4(a+b)(a-b) which is a 4n number however 46 is not divisible by 4. So no cases are possible
Problem Links -
3/05/2015 03:04:00 am
even number
,
number basics
,
number representation
,
Number System
,
odd number
,
Quantitative
,
theory
Number system|solution set 1|number basics,recurring decimals
meette
2/24/2015 05:11:00 am
number basics
,
Number System
,
problems
,
Quantitative
,
recurring decimal problems
,
recurring decimals
,
solutions
Number system|problem set 1|number basics,recurring decimals
meette
Hi everyone. Hope your preparations are going well. have curated a few good problems on number basics mainly recurring decimals. Solve them and post your answers in the comment box. I'll be putting the solution links soon. The following questions test your basics and will give you a clear idea of what you can expect in an exam.
Before solving go through the theory here.
Number System:number basics problem set 1:
Find the value of .1777..+ .131313...?
(1)5/15 (2) 17/55 (3) 31/99 (4) 147/990
Which among the following is a rational number?
(1) 2^∛8 (2) .122222…(3) .101001000…(4) both 1 and 2
What is the fraction form of 123.34565656....?
If N = .mnmnmn... and m and n are not necessarily distinct, how many values can the denominator take in N?
(1)5 (2) 1 (3) 3 (4) 4
2/24/2015 01:32:00 am
number basics
,
Number System
,
problems
,
Quantitative
,
recurring decimal problems
,
recurring decimals
Number System 1|Theory|number basics,recurring decimals
meette
This is the very first
post so I am super excited. I'll start with the absolute basics of number
system and go into details of every topic. Then I will be posting overwhelming
no of problems for you guys to solve.. Happy Learning :)
Classification of numbers.
So
numbers are broadly classified into real
numbers and imaginary numbers.
Real
numbers are those numbers which can be expressed in the number line whereas
imaginary numbers are those which cannot be expressed in the number line. They
don't exist in real life. For e.g. can a number like √-3 exist in real life?No
2/23/2015 11:35:00 am
Number System
,
Quantitative
,
theory
Subscribe to:
Comments
(
Atom
)